Physics
Fox
Summary
- The speed of an object is a measure of how fast it moves. Speed is defined by: \[ \text{speed} = \frac{ \text{distance} }{ \text{time} } \]
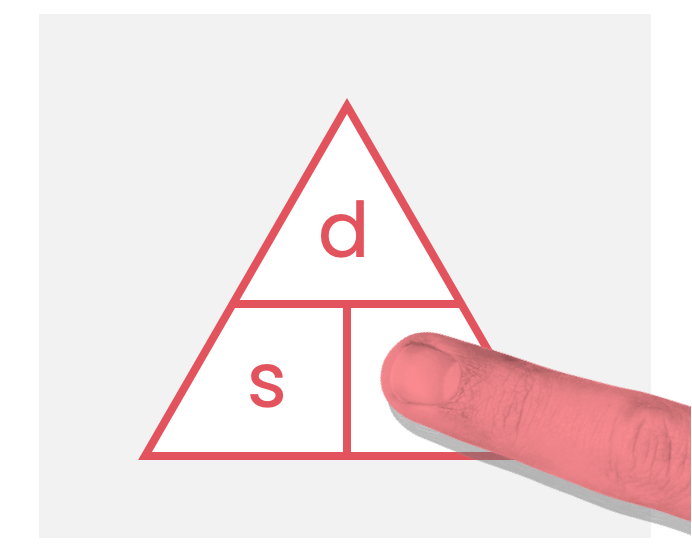
- This equation can be put into a formula triangle:
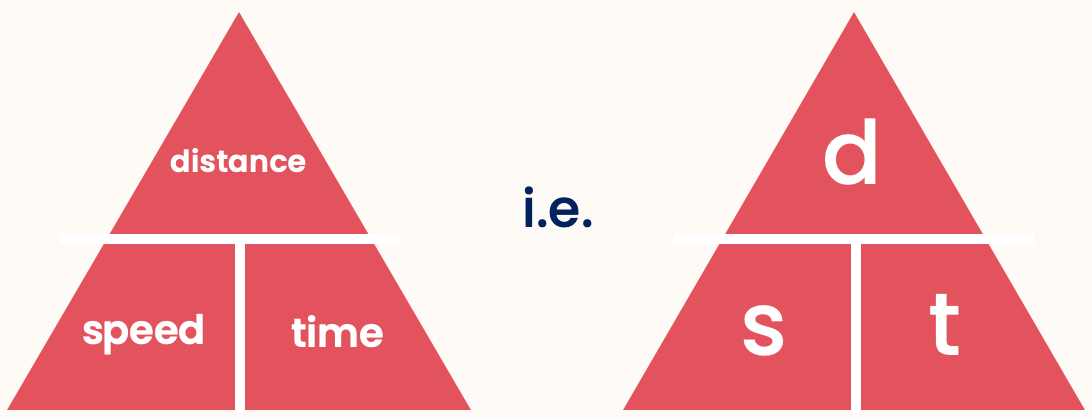
Use your finger to cover up the one you want to find, and the remaining two will show you how to find it. - The SI unit of speed is metres per second (m/s):
- Other units for speed include miles per hour (mph) and kilometres per second (km/s).

They ask me where the hell I'm going
At a thousand feet per second
Speed is something you've already come across is everyday life; if you're in a car you might be moving at a speed of 60 miles per hour (mph).

Today we're going to define what speed is, and show how to do calculations with it.
The speed of an object is a measure of how fast it moves.
Okay, so what's the difference between a fast thing and a slow thing?
A fast thing moves a longer distance than a slow thing does in the same amount of time.
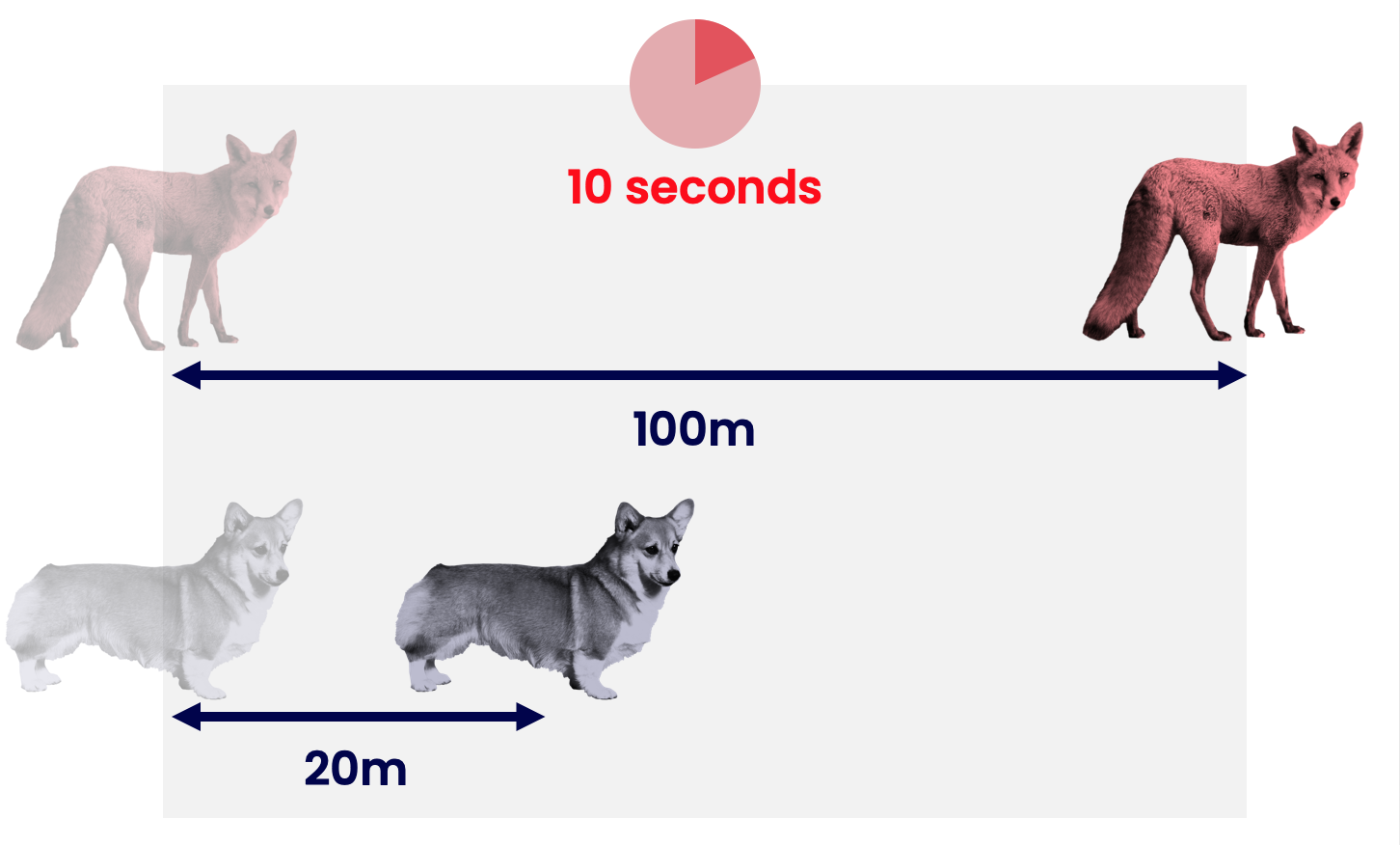
e.g. In \(10\) seconds, a quick fox might travel \(100\text{m}\), but a lazy dog might only travel \(20\text{m}\).
We define speed to be the distance travelled divided by the time taken:
\[ \text{speed} = \frac{ \text{distance} }{ \text{time} } \]So the fast fox has speed, \( \text{s} = \frac{\text{d} }{\text{t} } = \frac{100 \text{m} }{10 \text{s} } = 10 \text{ m/s} \)
and the lazy dog has speed, \( \text{s} = \frac{\text{d} }{\text{t} } = \frac{20 \text{m} }{10 \text{s} } = 2 \text{ m/s} \)
Note how the unit of speed (\( \text{ m/s} \) ) magically appeared when we calculated the speed!
As we have just found, the SI unit of speed is m/s:

m/s isn't the only unit of speed, it's just the scientific unit. On this page we've already mentioned two other units of speed: ‘feet per second’ and ‘miles per hour’. What all of these units have in common is that they all have the form: [distance unit] / [time unit]. They need to have this form because speed = distance / time !
NB: m/s is always spoken aloud as “metres per second”, like how mph is spoken as “miles per hour”. Any unit with a divide sign in the middle is spoken as “per”.
\( \text{speed} = \frac{ \text{distance} }{ \text{time} } \) can be written as a formula triangle:
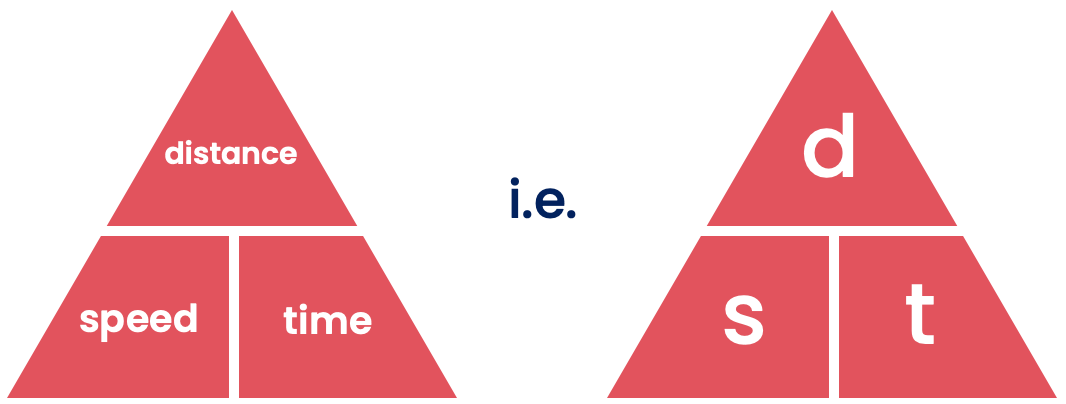
Many people find these useful. Here's how they work:
Use your finger to cover up the symbol you want to find, and the remaining two symbols will show you how to find it:
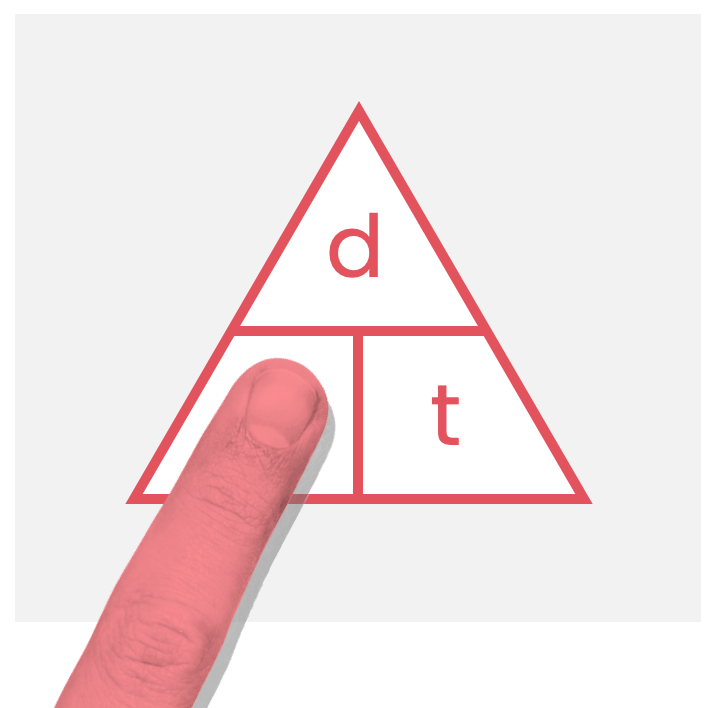
For example, if you want to find the speed, cover up \( s \) with your finger. We can see that \( d \) is on top of \( t \). Therefore, \( \text{s} = \frac{ \text{d} }{ \text{t} } \)!

Similarly, if we want to find the distance, cover up \( d \) with your finger. We can see that \( s \) is next to \( t \). Therefore, \( \text{d} = \text{s} \times \text{t} \) !
Let's solve some example questions using this method...
NB: A formula triangle can be used any time you have an equation which looks like A = BC or A = B/C. (You can do this because the triangle doesn't ‘know’ what the symbols inside it actually mean).Usain Bolt runs 24m in 2s. What is his speed?
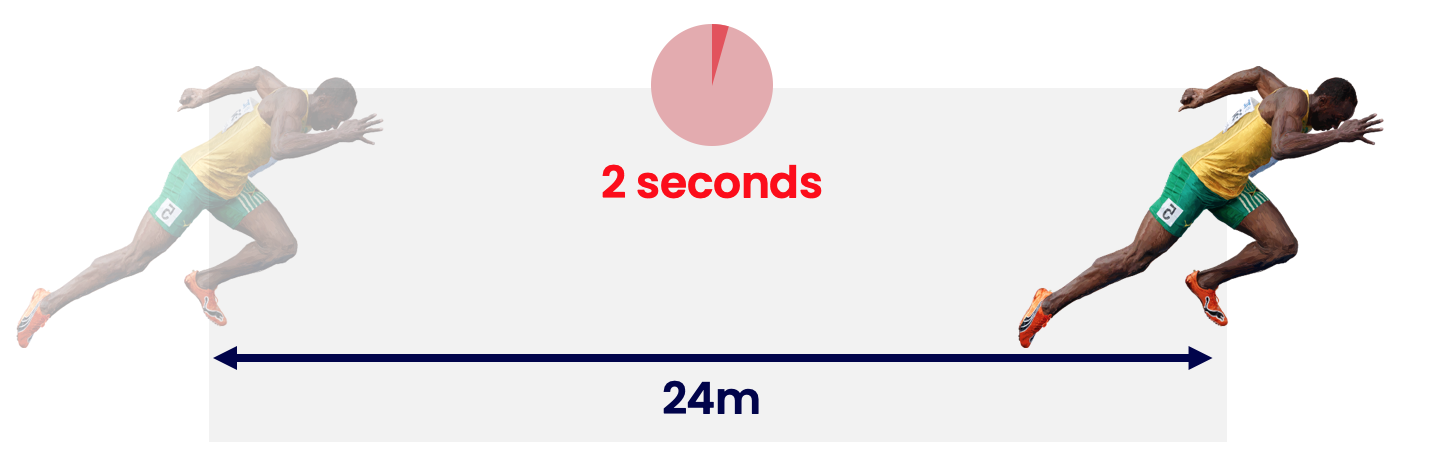
We can sum up this question as:
speed = ?
distance = 24m
time = 2s
Using the definition of speed, we know that speed = distance / time. Alternatively, we could cover up \( s \) on the formula triangle with our finger to reveal: \( \text{s} = \frac{ \text{d} }{ \text{t} } \).
Therefore, Usain Bolt's \( \text{speed} = \frac{24 \text{m} }{2 \text{s} } = 12 \text{ m/s} \).
That's absolutely R a p i d.

A drone travels at 15 m/s for 4 seconds. How far does it travel?
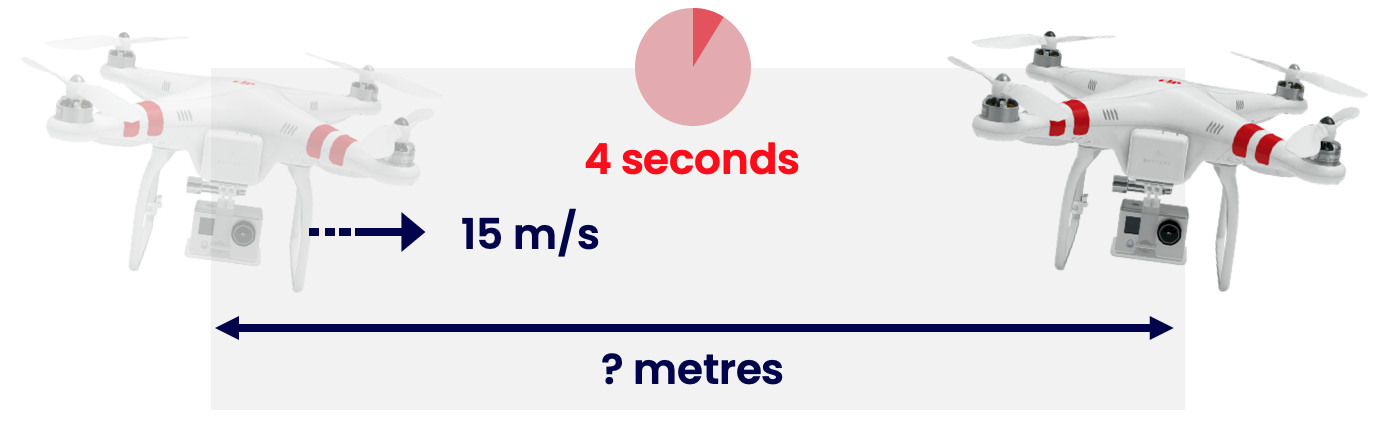
We can simplify this question as:
speed = 15m/s
distance = ?
time = 4s
We need a formula to get distance from speed and time. Covering up \( d \) on the formula triangle shows \( s \) and \( t \) next to each other. Therefore, \( \text{d} = \text{s} \times \text{t} \).

Therefore, the drone travels a distance \( \text{d} = 15 \text{m/s} \times 4\text{s} = 60 \text{m} \).
A tsunami wave travels at 200m/s. It is 10km away from the shore. How long until the tsunami reaches the shore?
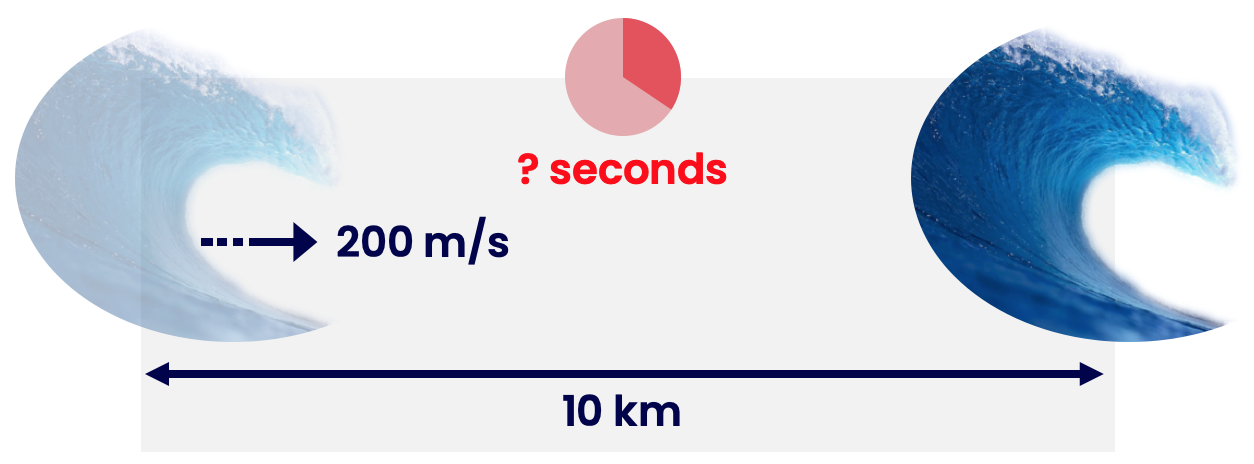
We can more succinctly write this question as:
speed = 200m/s
distance = 10km = 10,000m
time = ?
We need a formula to get distance from speed and time. Covering up \( t \) on the formula triangle shows \( d \) on top of \( s \). Therefore, \( \text{t} = \frac{ \text{d} }{ \text{s} } \).
Therefore, the time taken \( = \frac{ 10,000 \text{m} }{ 200 \text{m/s} } = 50 \text{s} \).
When we are just using SI units (m, s, m/s), things are relatively straightforward. Unfortunately in the real world, people will use all sorts of units that aren't SI units.
Consider the following question:
A Formula One racing car can travel 30 km in 5 minutes. What is its speed in m/s?
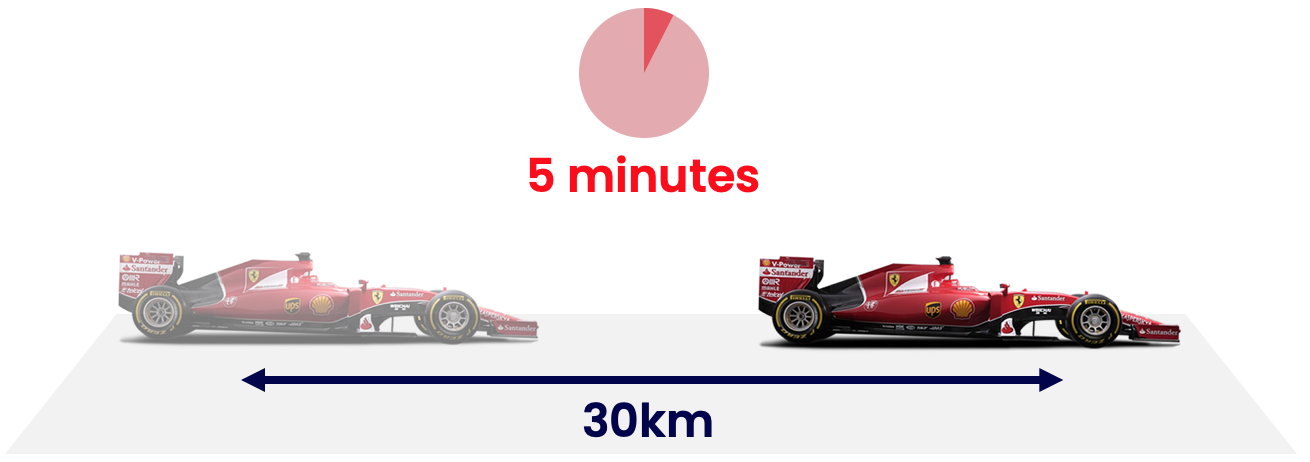
First, we approach this as we have done for the previous 3 examples:
1) Find the relevant formula: (speed = distance/time)
2) Find the relevant quantities in the formula: (distance = 30 km, time = 5 minutes).
3) Put these quantities into the formula: (speed = 30 km/5 mins = 6 km/minute).
However, we have come across a problem. Our speed is in units of km/minute, but the question wants this the answer in m/s !
To fix this issue, we need to add another step between 2) and 3): in order to get the speed in m/s, we need to get the distance in m, and the time in s.
For distance, this isn't so bad. 1km = 1000m, so 30km = 30,000m.
For time, we need to use that 1 minute = 60s. Therefore, 5 minutes = 5 × 60s = 300s. (Feel free to use a calculator for this.)
So our quantities (step 2) are now: distance = 30,000m, time = 300s.
Finally, we put this into our formula (speed = distance/time), to get speed = 30,000m / 300s = 100m/s.
The formula triangle is really a trick for doing something called rearranging formulae.
For example, when finding the distance an object moves, what we're really doing is multiplying \( \text{speed} = \frac{ \text{distance} }{ \text{time} } \) by time on both sides of the equation:
\( \text{s} = \frac{ \text{d} }{ \text{t} } \)
\( \text{s} \times \text{t} = \frac{ \text{d} }{ \text{t} } \times \text{t} \)
\( \text{s} \times \text{t} = \text{d} \times \frac{ \text{t} }{ \text{t} } \)
\( \text{s} \times \text{t} = \text{d} \)
\( \text{distance} = \text{speed} \times \text{time} \)
(Because \( \frac{ \text{t} }{ \text{t}} = 1 \).)
You'll use this technique in future when studying algebra in maths class.
Congratulations!
7 of 7 questions completed
+ ⭐️ collected.
Sign up (for free!) to:
• save your progress 📊
• create constellations✨
• customise your fox! 🦊







